欧拉路径和欧拉回路

  • 对于无向图，所有边都是连通的。

    （1）存在欧拉路径的充分必要条件：度数为奇数的点只能有0个或2个。

    （2）存在欧拉回路的充分必要条件：度数为奇数的点只能有0个。

  • 对于有向图，所有边都是连通。

    （1）存在欧拉路径的充分必要条件：要么所有的点出度均等于入度；要么除了两个点之外，其余所有点的出度等于入度，剩余的两个点：一个满足出度比入度多1（起点），一个满足入度比出度为1（终点）。

    （2）存在欧拉回路的充分必要条件：所有点的出度均等于入度。

随记：

在学习过程中，有几个困扰我的点，这里列一下方便回忆。 欧拉路径有如下两种形式，其余各种各样的形式都可以简化成这两种。

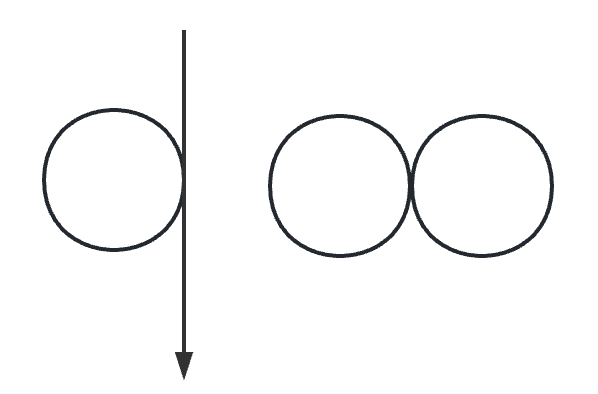
深搜加入边的顺序

在 dfs 过程中，从起点出发深搜，第一次回溯的地方必定是终点。在深搜过程中，需要将遍历过的边及时删除，防止重复遍历，复杂度退化成 $O(m^2)$ 。

以左图为例，如果按照深搜的过程加入所有的深搜到的边，那么这个环未被正常加入。 这里正常加入是指，如果我们回溯到交点处，再去遍历环上的边，这样就不是一笔画了。

按照深搜的顺序结束后再将当前遍历的边加入，一个未得到数学证明的猜想：以这种方式，每个点在你当前 dfs 栈中最多只会拓展 2 次（与这个点相连的边会在这个点的其他 dfs 栈中被遍历到）。

最后得到的是欧拉路径的逆序边，reverse 后即欧拉路径。

假设当前点是 i ，当前遍历的边的另一个点为 j 在执行完 dfs(j) 后，就将对应的边加入栈中。这是因为这里考虑 dfs(j) 是考虑将所有从 j 开始的边都遍历完毕。 如此，这条 i->j 的边就是当前顺序中遍历的最靠后的边。

故在加入边时，在每次 dfs 后就将这条边加入栈中，这是正确的。

深搜加入点的顺序

点的序列表示欧拉路径，路径中连续的两个点即表示一条边，故 点数 = 边数 + 1 。

依旧考虑 dfs 过程。当前点为 i ，而上述说明已经表明了可能会存在一个 dfs 栈中，一个点会遍历至多 2 条边。如果我们在一次 dfs 结束后就加入当前点 i ，看起来是没什么大问题的。

我们来考虑这个例子

n = 3, m = 3

每条边如下：
1 2
1 3
1 3

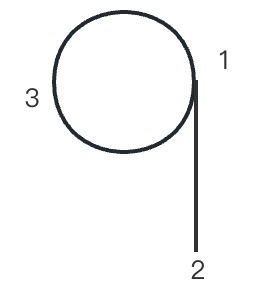
假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，加入点 2 ，此时序列为 [2]
  • 回溯到 1 ， 此时 dfs(1) 结束了一次，加入点 1，此时序列为 [2,1]
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，故加入点 1，序列为 [2,1,1]
  • 回溯到 3 ，此时 dfs(3) 结束了一次，加入点 3，此时序列为 [2,1,1,3]
  • 回溯到 1 ，此时 dfs(1) 结束了一次，加入点 1，此时序列为 [2,1,1,3,1]

这里连续两个 1 显然是错误的，说明我们这里加点顺序是有问题的。

那么这里相较于加入边有什么区别呢？再来模拟下加入边的过程：

假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，结束
  • 回溯到 1 ， 此时 dfs(1) 结束了一次，加入边 1->2，此时序列为 [1->2]
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，结束
  • 回溯到 3 ，此时 dfs(3) 结束了一次，加入边 3->1，此时序列为 [1->2,3->1]
  • 回溯到 1 ，此时 dfs(1) 结束了一次，加入边 1->3，此时序列为 [1->2,3->1,1->3]

这里的加边序列为：[1->2,3->1,1->3]，即 [2<-1, 1<-3, 3<-1]

上述的加点序列为：[2,1,1,3,1]，正确的加点序列为：[2, 1, 3, 1]

这里问题在于我们多加入了一个 1 ，这两个 1 都是在 dfs 结束的时候加入的，而其他的点加入存在情况为这个点不存在其他的边时，加入这个点。

如果修改为这种情况，再来模拟下加点的过程：

假设起点为 1

  • 首先遍历了1->2 这条边
  • 2 没有其他的边，加入点 2 ，此时序列为 [2]
  • 回溯到 1 ， 此时 dfs(1) 结束了一次
  • 1 继续遍历边 1->3 （两条边随意，对结果不影响）
  • 3 遍历其唯一的一条边 3->1
  • 1 此时没有其他的边，故加入点 1，序列为 [2,1]
  • 回溯到 3 ，3 此时没有其他的边，故加入点 3，序列为 [2,1,3]
  • 回溯到 1 ， 1 此时没有其他的边，故加入点 1，序列为 [2,1,3,1]

如此就是正确的了。

但这里还没有搞清楚加点的具体的含义。

不同于加边，每条边在遍历后立马被删除，所以边在 dfs 完毕后立马加入是可以的。

假设当前点为 vertex，当前遍历完边 edge1，加入 edge1 后，假设当前 dfs 栈还可以遍历一条边 edge2，则说明 edge2 在欧拉路径中，通过 edge2，到达了 vertex，然后再通过 edge1 出去。

对于加点来说，每个点的加入需要斟酌，直观的想法就是按照加边的顺序加点。但是这会存在上述模拟中的情况，多加入了一些点。

之前说过，每个点至多会走两条边 e1 和 e2，这是因为 e1 会走到终点，然后回溯。如果说通过 e1 又可以一直深搜走回这个点，那么这就是一条完整的路径。回溯过程中按照这个顺序加点即可。

考虑两种情况：

  1. 从当前点 vertex 可以直接从一条边出发走完剩余未走的所有边，并且回到 vertex，此时我们只需要在回溯前（return 之前）加点即可。

  2. 从当前点 vertex 从一条边走到了终点，然后需要回溯继续走剩余未走的边。对于从终点回溯到当前点 vertex 的部分，假设这些点已经不存在其他的边了，那么只需要在他们回溯前（return 之前）加点即可。

    这些未走的边，我们继续从 vertex 出发，必然是一个环。因为是从 vertex 继续出发走这个环，必然最后会回到 vertex。考虑一个环的加边顺序，遍历完这个环后，依次回溯加入环的边，对于第一个加入的边，实际上是遍历环结束后到达 vertex 的边，而在正序的欧拉路径中，这条边之后就会继续从 vertex 深搜到终点，所以说，这条边紧接着之后的深搜到终点的路径，对应到这个图上是：从[3->1, 1->2]。

    而这里的 1 只能被加入 1 次，上述错误的加点顺序中，我们在回溯到 vertex 时加入了一次，然后遍历完这个环后回溯又加入了一次，导致这里加入了两次。

    我们需要清楚的是，这里环的回溯第一次加的边 3->1 ，之前加的边为 1->2 ，使得序列变成了 [1->2, 3->1] 正序欧拉路径即为：[3->1, 1->2]。

    冲突在于：整个欧拉路径用边表示和用点表示的数量关系为：点数 = 边数 + 1，每条边都可以用 到达点 来表示，最后再加上一个整个路径的起点即可。

    所以我们这下清楚了，我们是使用每条边的到达点作为这条边的代表。如此，一个点在一次 dfs 栈中只有一次作为到达点的可能，即这个点遍历完了其所有还存在的边后（此时相当于我将所有其他的环都遍历完了）。因为我这条边先遍历到，那么我就应该最后加入这条边，这样在欧拉路径的顺序才是正确的。

综上：

在回溯前加点，每个点表示的是边对应的到达点。而我们可以认为 dfs(start) 中这个起点 start 也是从某个点过来的，回溯过程中也是最后将其加入欧拉路径中，这样整体的逻辑就说得通了。

总结

在跑欧拉路径时，加边和加点的问题，本质在于这条边是什么边： 假设我们当前在点 a 经过边 edge 到达了点 b，而我们到达 a ，是从 prea 经过 pre_edge 到达了 a

  • 对于加边，我们从 a 经过 edge 到达了 b 后，从 b 出发的所有点遍历完毕后再加入点 a，是指 edge 这条边可以到达的其他边已经结束，而 edge 这条边是我们遍历完其之后的边的起始边。

  • 对于加点，我们从 prea 经过 pre_edge 到达 a，再从 a 开始遍历其所有的边去深搜，深搜结束后，我们再将 prea->a 这条 pre_edge 边加入到序列中，加入的形式是将 a 这个 prea 的到达点加入到序列中。

    我们在调用 dfs(start) 时，可以认为我们是从一个 虚拟点 virtual_vertex 经过虚拟边virtual_edge 到达了 start ，所以这样的话也可以将 start 作为边的到达点了。

故我们的加边和加点顺序为：

  • 对于加边的问题，应该在一次边的 dfs 结束后就将当前遍历走的这条边加入。
  • 对于加点的问题，应该在所有当前点的 dfs 结束后才将当前点 vertex 加入，这个点 vertex 代表的是走到 vertex 这个点的 edge 的到达点。

疑惑

这里不用起点来代表每条边的原因：在 dfs 时，我们并不知道哪个点是终点（并不是所有的欧拉路径都存在两个度为奇数的起点和终点，欧拉回路这种欧拉路径所有的度数都是偶数），但是我们第一次开始 dfs 的点就是起点，最后回溯回来也可以顺利地将其加入欧拉路径的点序列中。

例题1

P7771 【模板】欧拉路径

示例代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
const int M = 200010;
multiset<int> h[N];
int din[N], dout[N];
int ans[M], cnt;
int n, m;

void dfs(int u) {
    while (!h[u].empty()) {
        int v = *h[u].begin();
        h[u].erase(h[u].begin());
        dfs(v);
    }
    ans[++cnt] = u;
}

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        h[a].insert(b);
        dout[a] += 1;
        din[b] += 1;
    }

    int act[2] = {0, 0};
    int start = 0;
    for (int i = 1; i <= n; ++i) {
        if (din[i] == dout[i] + 1) {
            act[0] += 1;
        } else if (dout[i] == din[i] + 1) {
            start = i;
            act[1] += 1;
        } else if (din[i] != dout[i]) {
            puts("No");
            return 0;
        }
    }

    if (act[0] != act[1] || act[0] > 1) {
        puts("No");
        return 0;
    }

    if (start == 0) {
        for (int i = 1; i <= n; ++i) {
            if (dout[i] == din[i] + 1) {
                start = i;
                break;
            } else if (din[i] == dout[i] && start == 0) {
                // 字典序最小，如果不存在 dout[i]==din[i]+1的起点，那么就选择字典序最小的
                start = i;
            }
        }
    }

    dfs(start);

    for (int i = cnt; i >= 1; --i) printf("%d%c", ans[i], " \n"[i == 1]);

    return 0;
}

例题2

1184. 欧拉回路

示例代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

#include <bits/stdc++.h>
using namespace std;

const int N = 100010;
const int M = 400010;

int h[N], e[M], ne[M], idx;
bool used[M];
int ans[M >> 1], cnt;
int din[N], dout[N];
int n, m, type;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) {
    while (h[u] != -1) {
        // 删边
        int i = h[u];
        h[u] = ne[i];
        
        // 标记用过的边和其反向边，used[i]=true其实用不到了，因为这条边已经被删除了
        if (used[i]) continue ;
//        used[i] = true;
        if (type == 1) used[i ^ 1] = true;

        dfs(e[i]);

        int t = i + 1;
        if (type == 1) {
            t = i / 2 + 1;
            if (i & 1) t = -t;
        }
        ans[++cnt] = t;
    }
}

int main()
{
    scanf("%d", &type);
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);

    for (int i = 1; i <= m; ++i) {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
        if (type == 1) add(b, a);
        din[b] += 1;
        dout[a] += 1;
    }

    if (type == 1) {
        for (int i = 1; i <= n; ++i) {
            if ((din[i] + dout[i]) % 2 == 1) {
                puts("NO");
                return 0;
            }
        }
    } else {
        for (int i = 1; i <= n; ++i) {
            if (din[i] != dout[i]) {
                puts("NO");
                return 0;
            }
        }
    }

    for (int i = 1; i <= n; ++i)
        if (h[i] != -1) {
            dfs(i);
            break;
        }

    if (cnt < m) {
        puts("NO");
        return 0;
    }

    puts("YES");
    for (int i = cnt; i >= 1; --i) printf("%d%c", ans[i], " \n"[i == 1]);

    return 0;
}