强连通分量的定义

强连通分量是对于有向图来说的。通常，我们在对有向图做一些操作时，都是指在有向无环图（DAG, Directed Asyclic Graph） 来说的。所以将一个有向有环图转换为有向无环图是很有必要的。

对于一个有向图 $G(V, E)$ ，对于任意两个点 $x\in V, y\in V, x \neq y$ ，既存在 $x$ 到 $y$ 的路径，也存在 $y$ 到 $x$ 的路径，则称这个图是强连通图。

强连通分量 （SCC, Strongly Connected Component）是指一个有向图的极大强连通子图。

即：对于每个分量，在其中加入其他点，使得点数最多，且任意两个点都有一条互相可达的路径。

对于一个有向图，每个点都属于一个强连通分量，求出一个有向图的所有的强连通分量，将每个强连通分量看成一个点，这称为缩点。缩点后，就一定是一个有向无环图。

那么问题就转换为了如何求强连通分量。

求强连通分量的相关介绍

这里抛出几个概念：

dfn

dfn[i] 表示先按照 dfs 遍历点的先后顺序，第 i 个点是在第 dfn[i] 次访问一个新点时被访问到的，也叫作访问时间戳。

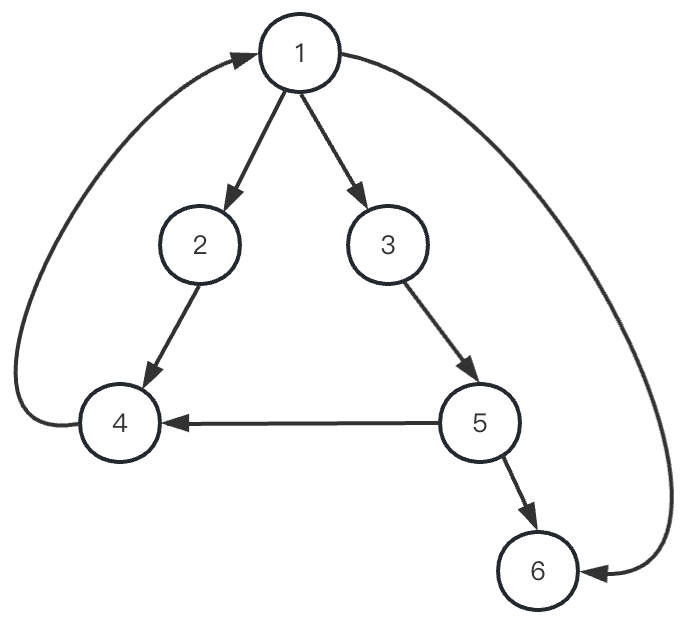上面这个图，从 1 号点开始 dfs ，则 dfn 下图所示：

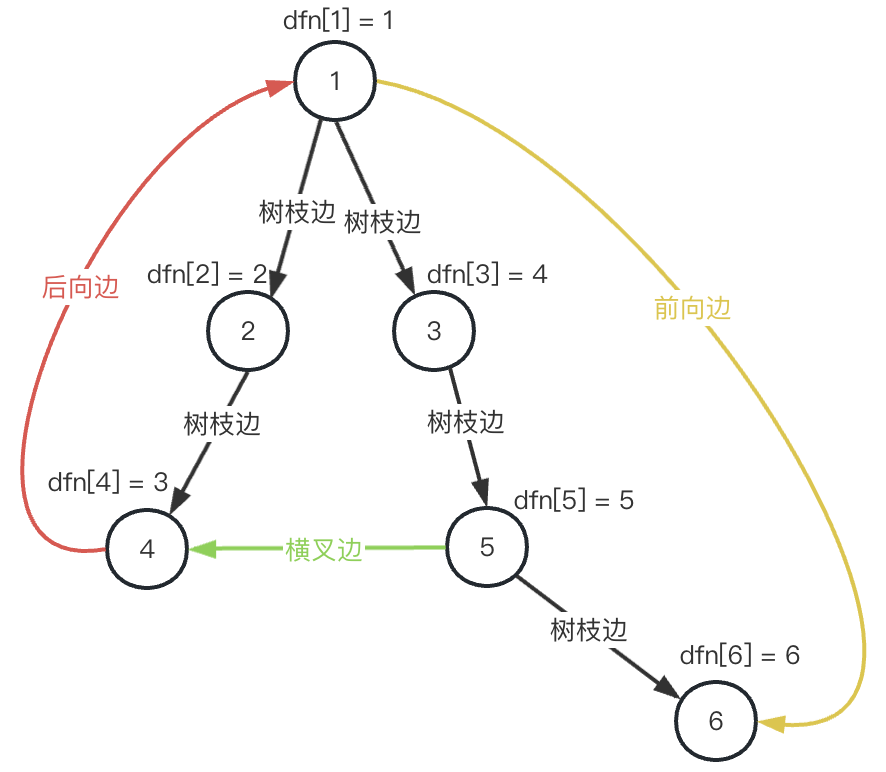
即 dfs 遍历点的顺序为：1->2->4->3->5->6

以此，我们来介绍这个 dfs 搜索树上的四种边。

  • 树枝边 (x, y)，如图黑色边 ，在搜索树上，点 x 是点 y 的父亲节点，且 dfn[x] < dfn[y]
  • 前向边 (x, y)，如图黄色边 ，在搜索树上，点 x 是点 y 的祖先节点，且 dfn[x] < dfn[y]
  • 后向边 (x, y)，如图红色边 ，在搜索树上，点 y 是点 x 的祖先节点，且 dfn[x] > dfn[y]
  • 横叉边 (x, y)，如图绿色边 ，在搜索树上，两者不存在祖先和子辈的关系，即这两个点在 dfs 树上是他们 lca 下的不同子树的，且 dfn[x] > dfn[y]

low

low[u] 表示从 u 开始，遍历点 u 的子树，可以到达的最小的时间戳。

  • 第一种情况：点 u 的儿子 v 还未被遍历，此时更新方式为 low[u] = min(low[u], low[v])
  • 第二种情况：点 u 的儿子 v 已经在之前作为其他点的子树被遍历过了，但是还未结束遍历，此时更新方式为 low[u] = min(low[u], dfn[v])， u->v 要么是后向边，u->v 要么是横叉边，故此时通过 dfn[v] 去更新 low[u]，一定有更新后的 low[u] < dfn[u]。故：如果 v 在一个环中，u 也可以加入这个环，与他们一起构成一个连通分量。

事实上，这里取 low[u] = min(low[u], low[v]) 对于求强连通分量是无影响的，个人认为是正确的。 因为在 tarjan 这个算法的论文中的定义为：low 是最多通过一条反向边能到达的最小 dfn ，我们这里将 u->v 认为是一条反向边。但是实际上这个 low 最多通过一条反向边的限制并没有什么用，所以这里无所谓。

当然，在求解无向图的双连通分量时，这样更新 low 就会出现错误，所以这样的正确更新仅存在于有向图的强连通分量的求解。

为了不出错，也为了尊重作者，建议第二种情况还是使用论文中的更新方式，即 low[u] = min(low[u], dfn[v]) 来更新。

写完无向图的双连通分量后，再来解释 这块实际会对求解产生错误的情况，实际是在针对求解 无向图的边双连通分量 的时候的，为了避免错误，建议还是统一一下。

stack

stack 表示栈中的元素，这个栈是存储从当前 u 开始的子树遍历到的所有点，当遍历结束后，如果发现 dfn[u] == low[u] ，则 u 是其所在连通分量 SCC 中 dfn 最小的点，那么就说明已经找完了 SCC 中所有的点，pop 出栈直到 pop 出 u 截止，即 SCC 中所有的点。

代码模板

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

// tarjan 模板

vector<int> g[N]; // vector 存储图
int dfn[N], low[N], tim;
int stk[N], top;
bool in_stk[N];

int scc[N]; // scc[u] 表示点 u 所在的 SCC 的编号
int sz[N];  // sz[i] 表示编号为 i 的 SCC 的大小
int scc_cnt; // 表示 SCC 的数量

void tarjan(int u) {
    dfn[u] = low[u] = ++tim;
    stk[++top] = u;
    in_stk[u] = true;

    for (int v: g[u]) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (in_stk[v]) {
            low[u] = min(low[u], dfn[v]);
        }
    }

    if (dfn[u] == low[u]) {
        int y; ++scc_cnt;
        do {
            y = stk[top--];
            in_stk[y] = false;
            scc[y] = scc_cnt;
            sz[scc_cnt] += 1;
        } while (y != u);
    }
}

for (int i = 1; i <= n; ++i) 
    if (!dfn[i]) tarjan(i);