无向图的双连通分量有两种:
- 边的双连通分量(E-DCC)
- 点的双连通分量(V-DCC)
边的双连通分量定义
首先引入桥的概念,一个无向连通图的无向边,如果将这条边删除,这个无向图就不连通了,则这条边就是桥,桥也叫割边。
极大的,不含有桥的连通块,就称为边的双连通分量。
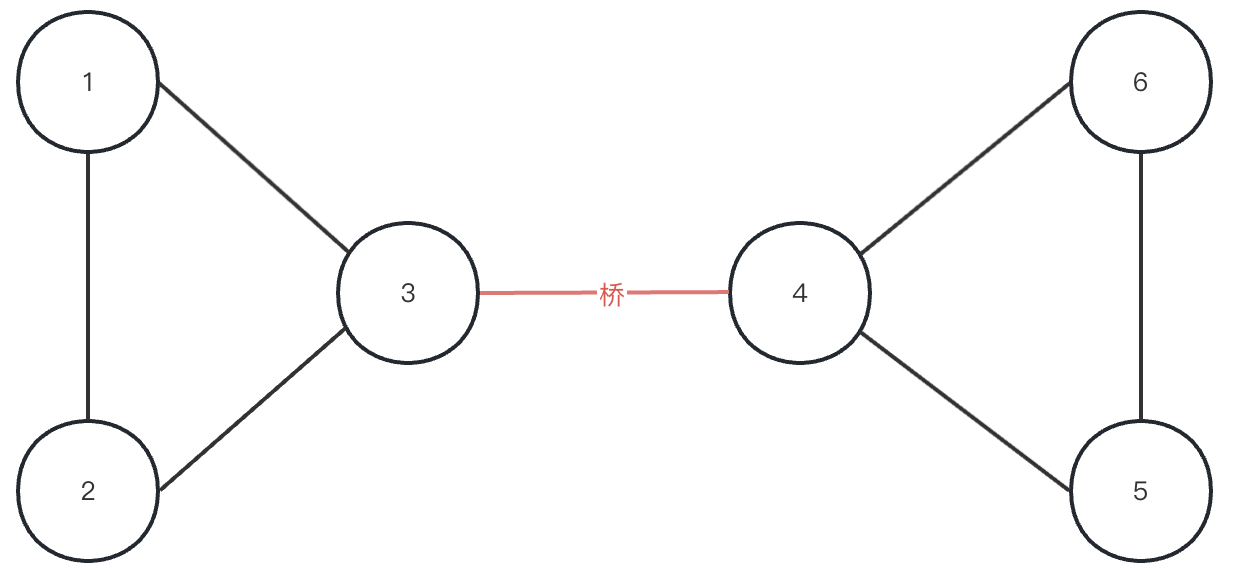
如上图所示,3-4 之间的红色边就是桥。
点的双连通分量定义
首先引入割点的概念,一个无向连通图中,如果将一个点删除后,这个无向图就不连通了,则这个点就是割点。
极大的,不含有割点的连通块,就称为点的双连通分量。
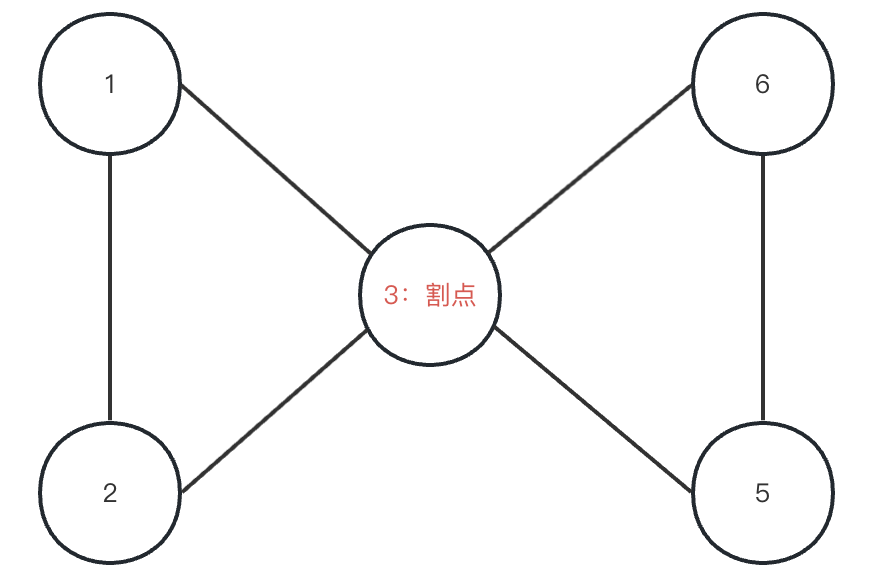
如图所示,3 号点就是割点。
每个割点,都至少属于两个双连通分量。就比如上面这个图,3号点既属于 {1,2,3} 这个点的双连通分量,也属于{3,4,5} 这个点的双连通分量。
此外,对于点的双连通分量来说,有一些反直觉的东西。
比如对于两个割点之间的边,就一定是桥,这是错的。
对于如下这张图来说,3 是割点,4也是割点,3-4 这条边是桥。

但是对于如下这张图来说,3 是割点,4 也是割点,3-4 这条黄色边就不是桥。
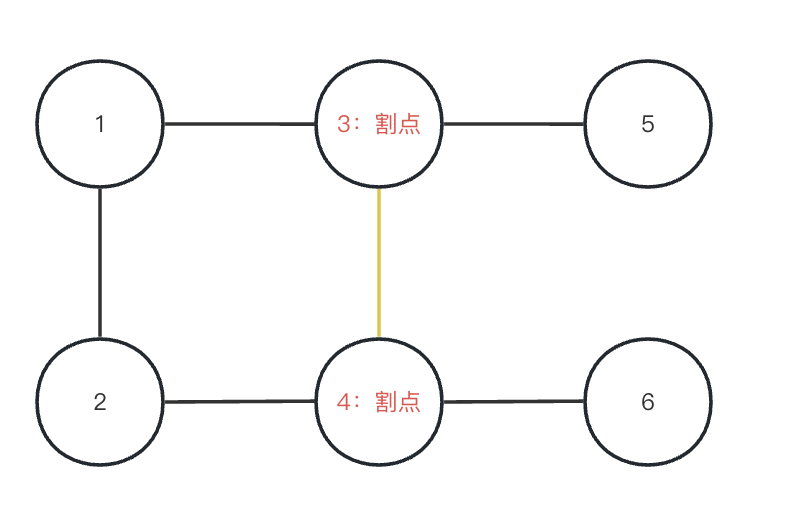
同时,有桥也不一定有割点。
如下图所示,1-2 这条边是桥,但是 1 和 2 都不是割点,删除 1 或者 2,图中都只剩下了一个点。

总结得出:
有割点不一定有桥,有桥也不一定有割点。割点和桥没有什么必然联系。
点连通分量也不一定是边连通分量,边连通分量也不一定是点连通分量。
简要总结
-
除了下面这张点的双连通分量,其他任意的点的双连通分量都满足,任意两点之间都满足至少两条点的不重复路径。

-
无向图中任意一个割点都至少存在两个点的双连通分量中。
-
无向图中任意一个不是割点的点,都只存在于一个点的双连通分量中。
点的双连通分量求解
dfn[x] 表示第一次访问 x 时,是访问的第 dfn[x] 个点low[x] 表示 x 从所有的儿子点出发,可以访问到的最小的 dfn
考虑当前点为 u ,枚举的边为 edge ,edge 的另一个点为 v。
如果 low[v] >= dfn[u] ,考虑如下情况:
-
如果 u 是根节点,将 u 删除后,至少有两个子节点满足 low[v1] >= dfn[u] && low[v2] >= dfn[u],则 u 是割点。
这里需要至少两个子节点是因为:当 root = u ,在任何情况下,low[root_son] >= dfn[root],如果 root 只有一个儿子,则删除 root 后,图依旧连通。
-
如果 u 不是根节点,令 root 为根节点,则说明 v 无法通过儿子来到达 root ,因为 low[v] >= dfn[u] > dfn[root] ,则 u 是割点。
来看道题:电力
题意:
给定一个由 n 个点 m 条边构成的无向图,请你求出该图删除一个点之后,连通块最多有多少。
数据范围:$1\leq n\leq 10000, 1\leq m\leq 15000$
题解:
对于无向图进行缩点,然后每个割点删除后,连通块才有可能增多。故问题就是在枚举删除每个割点后,连通块的数量。
这里并未说明这个图为无向连通图,所以需要遍历每个点。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
const int M = 30010;
int n, m;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfn[N], low[N], tim;
int ans, root;
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
int cnt = 0;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) cnt += 1;
} else low[u] = min(low[u], dfn[v]);
}
if (u != root) cnt += 1;
ans = max(ans, cnt);
}
int main()
{
while (~scanf("%d%d", &n, &m) && (n || m)) {
for (int i = 0; i < n; ++i) dfn[i] = low[i] = 0, h[i] = -1;
idx = tim = 0;
for (int i = 1, a, b; i <= m; ++i) {
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
}
ans = 0;
int cnt = 0;
for (root = 0; root < n; ++root)
if (!dfn[root]) {
cnt += 1;
tarjan(root);
}
printf("%d\n", ans + cnt - 1);
}
return 0;
}
|
考虑无向图的点双连通分量缩点
首先,不同于边的双连通分量和有向图的强连通分量的缩点,点的双连通分量缩点过程是,对于每个点的双连通分量,如果其内部存在割点,则向其内部每个割点连一条边。
之前说过,每个割点至少属于两个点的双连通分量。
简单证明下:如果一个割点属于 0 个点的双连通分量,这显然是不可能的。如果一个割点属于 1 个点的双连通分量,则将该割点去除后,原图依旧是连通的,只是去掉了这个割点而已。所以,每个割点至少属于两个点的双连通分量,这样在将割点去除后,原图就不连通了。
如此,我们上述缩点的方式,就满足了每个割点都与其所在的所有的点的双连通分量连了一条边,最坏情况下缩点后的图中的点数是原图的 2 倍。
注意,这里是无向图缩点后的核心!!!
每个无向连通图进行缩点后,一定是一棵树!!!(这里我们不考虑不存在割点的无向连通图。)
其中,原图中的割点在缩点后的图中对应的点,度数至少为 2。
因为新图一定是一棵树,我们可以以任意一个割点在缩点后的图中对应的点作为新图的根,以此来解决其他问题。
考虑无向图的点双连通分量求解
对于当前点 u ,遍历其所有儿子,假设当前遍历的儿子为 v ,v 遍历结束后,如果说 low[v] >= dfn[u] ,那么如果 u 不为根或者 u 为根但是至少有两个子树必须通过 u 才能互相到达,那么 u 为割点。对于这样的 v ,均将 u 作为其点的双连通分量中的一部分。同时,u 也可能作为其父节点所在点双中的一部分。之前的证明:关于如何求割点
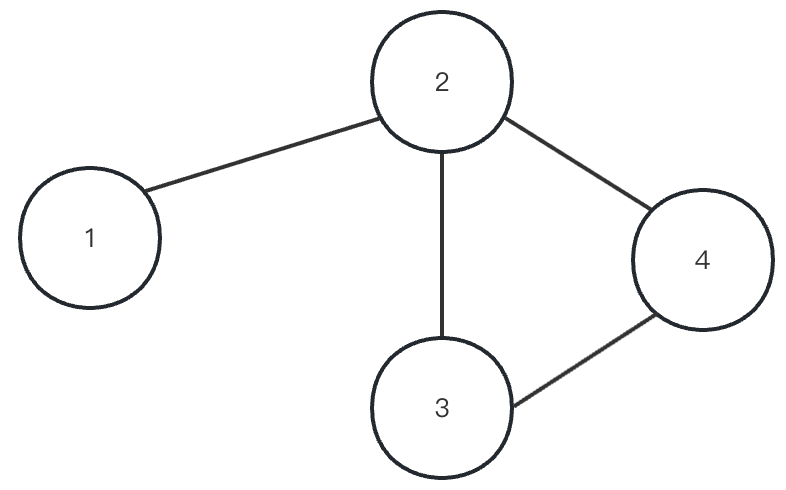
如下图所示:从 1 开始遍历,在遍历完 2 后,2 作为 {2, 3, 4} 这个点的双连通分量的一部分,但是也作为 {1, 2} 这个点的双连通分量的一部分。所以求解点的双连通分量的过程如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
if (low[v] >= dfn[u]) {
// 有一个新的点双是包含 v,所以 vdcc_cnt += 1
vdcc_cnt += 1;
// 上述所说的
if (u != root || vdcc_cnt > 1) u 是割点;
// 类似scc的出栈,求出当前 vdcc 中的所有点
将栈中元素弹出,直至栈顶为 v 为止;
/*
u 也是当前这个 vdcc 中的一部分,但是对于下面这个图来说,1 不属于 {2, 3, 4} 这个 vdcc
Q:我们仍然按照这个做法去做,是对的吗?
A:是对的,如果说 u 不属于 v 所在的 vdcc ,那么说明 low[v] > dfn[u] ,
在 v 的 dfs 栈中,就会将其所有的子树的 vdcc 都求解完毕并弹出栈。
等到 v 的 dfs 栈结束,回溯到 u 遍历 v 这个点时,这个 v 的子树构成的 vdcc 已经被弹出了,
所以 u 加入的 vdcc ,是其与 v 的。
只不过当 low[v] == dfn[u] 时,v 的子树可以到达 u ,那么他们一起构成一个 vdcc 。
*/
将 u 加入这个 vdcc 中;
}
|
来看道题:396. 矿场搭建
题解:
对于这块的分析为:
- 对于没有割点的连通块,如果是孤立点,则为需要 1 个逃生通道,否则需要 2 个。
- 对于有割点的连通块,进行 vdcc 缩点,缩点后的图为一棵树。
- 以任意一个割点为根,则每个 vdcc 一定是叶子。
- 如果叶子相连的割点坍塌,则叶子中的点无法逃生,所以每个叶子中需要有一个逃生通道,且该逃生通道不能是与其相连的割点(但是,我们需要知道的是,我们在 vdcc 的缩点,是将割点和其所在的 vdcc 连边了,故这个点一定不会是割点,因为已经是一个 vdcc 了)。
- 如果割点非叶子非割点的 vdcc 中的一点坍塌,该 vdcc 中的其他点一定可以通过割点到达其他叶子,故无需单独逃生通道。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
|
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N = 1010, M = 1010;
int n, m;
int h[N], e[M], ne[M], idx;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dfn[N], low[N], tim;
int stk[N], top;
int dcc_cnt;
vector<int> dcc[N];
bool cut[N];
int root;
void tarjan(int u) {
dfn[u] = low[u] = ++tim;
// 孤立点
if (u == root && h[u] == -1) {
dcc_cnt += 1;
dcc[dcc_cnt].emplace_back(u);
return ;
}
// 去除孤立点后再添加进去,否则孤立点会被加入到其他连通块的vdcc中
stk[++top] = u;
int cnt = 0;
for (int i = h[u]; i != -1; i = ne[i]) {
int v = e[i];
if (!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
cnt += 1;
if (u != root || cnt > 1) cut[u] = true;
// 弹出栈,直到弹到 v ,但是 v 和 u 可能作为一个 vdcc,所以还需要把 v 加回来
dcc_cnt += 1;
int y;
do {
y = stk[top--];
dcc[dcc_cnt].emplace_back(y);
} while (y != v);
dcc[dcc_cnt].emplace_back(u);
}
} else {
low[u] = min(low[u], dfn[v]);
}
}
}
int main()
{
int T = 1;
while (~scanf("%d", &m) && m > 0) {
for (int i = 1; i <= dcc_cnt; ++i) dcc[i].clear();
memset(dfn, 0, sizeof dfn);
memset(h, -1, sizeof h);
memset(cut, false, sizeof cut);
idx = tim = n = top = dcc_cnt = 0;
for (int i = 1; i <= m; ++i) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
add(b, a);
n = max({n, a, b});
}
for (root = 1; root <= n; ++root) {
if (!dfn[root]) tarjan(root);
}
int res = 0;
ull num = 1;
for (int i = 1; i <= dcc_cnt; ++i) {
int cnt = 0;
for (int j: dcc[i])
if (cut[j]) cnt += 1;
if (cnt == 0) {
if (dcc[i].size() > 1) res += 2, num *= (dcc[i].size() - 1) * dcc[i].size() / 2;
else res += 1;
} else if (cnt == 1) {
res += 1, num *= dcc[i].size() - 1;
}
}
printf("Case %d: %d %llu\n", T++, res, num);
}
return 0;
}
|
参考
点双连通分量&边双连通分量详解

 如图所示,3 号点就是割点。
如图所示,3 号点就是割点。




